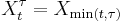Stopping time
In probability theory, in particular in the study of stochastic processes, a stopping time (also Markov time) is a specific type of “random time”.
The theory of stopping rules and stopping times can be analysed in probability and statistics, notably in the optional stopping theorem. Also, stopping times are frequently applied in mathematical proofs- to “tame the continuum of time”, as Chung put it in his book (1982). Stopping times are hitting times.
Contents |
Definition
A stopping time with respect to a sequence of random variables X1, X2, ... is a random variable  with the property that for each t, the occurrence or non-occurrence of the event
with the property that for each t, the occurrence or non-occurrence of the event  = t depends only on the values of X1, X2, ..., Xt. In some cases, the definition specifies that Pr(
= t depends only on the values of X1, X2, ..., Xt. In some cases, the definition specifies that Pr( < ∞) = 1, or that
< ∞) = 1, or that  be almost surely finite, although in other cases this requirement is omitted.
be almost surely finite, although in other cases this requirement is omitted.
Another, more general definition may be given in terms of a filtration: Let 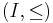 be an ordered index set (often
be an ordered index set (often 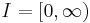 or a compact subset thereof), and let
or a compact subset thereof), and let 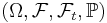 be a filtered probability space, i.e. a probability space equipped with a filtration. Then a random variable
be a filtered probability space, i.e. a probability space equipped with a filtration. Then a random variable 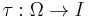 is called a stopping time if
is called a stopping time if 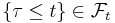 for all
for all  in
in  . Often, to avoid confusion, we call it a
. Often, to avoid confusion, we call it a 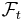 -stopping time and explicitly specify the filtration. Speaking concretely, for
-stopping time and explicitly specify the filtration. Speaking concretely, for  to be a stopping time, it should be possible to decide whether or not
to be a stopping time, it should be possible to decide whether or not 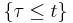 has occurred on the basis of the knowledge of
has occurred on the basis of the knowledge of 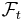 , i.e., event
, i.e., event 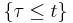 is
is 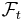 -measurable.
-measurable.
Stopping times occur in decision theory, in which a stopping rule is characterized as a mechanism for deciding whether to continue or stop a process on the basis of the present position and past events, and which will almost always lead to a decision to stop at some time.
Examples
To illustrate some examples of random times that are stopping rules and some that are not, consider a gambler playing roulette with a typical house edge, starting with $100:
- Playing one, and only one, game corresponds to the stopping time
 = 1, and is a stopping rule.
= 1, and is a stopping rule. - Playing until he either runs out of money or has played 500 games is a stopping rule.
- Playing until he is the maximum amount ahead he will ever be is not a stopping rule and does not provide a stopping time, as it requires information about the future as well as the present and past.
- Playing until he doubles his money (borrowing if necessary if he goes into debt) is not a stopping rule, as there is a positive probability that he will never double his money. (Here it is assumed that there are limits that prevent the employment of a martingale system, or a variant thereof, such as each bet being triple the size of the last. Such limits could include betting limits but not limits to borrowing.)
- Playing until he either doubles his money or runs out of money is a stopping rule, even though there is potentially no limit to the number of games he plays, since the probability that he stops in a finite time is 1.
Hitting times can be important examples of stopping times. However, while it is relatively straightforward to show that all stopping times are hitting times (see Fischer (2011)), it can be much more difficult to show that a certain hitting time is a stopping time. The latter types of results are known as the Début theorem.
Localization
Stopping times are frequently used to generalize certain properties of stochastic processes to situations in which the required property is satisfied in only a local sense. First, if X is a process and  is a stopping time, then X
is a stopping time, then X is used to denote the process X stopped at time
is used to denote the process X stopped at time  .
.
Then, X is said to locally satisfy some property P if there exists a sequence of stopping times  n, which increases to infinity and for which the processes
n, which increases to infinity and for which the processes 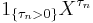 satisfy property P. Common examples, with time index set I = [0,∞), are as follows;
satisfy property P. Common examples, with time index set I = [0,∞), are as follows;
- (Local martingale) A process X is a local martingale if it is càdlàg and there exists a sequence of stopping times
 n increasing to infinity, such that
n increasing to infinity, such that 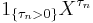 is a martingale for each n.
is a martingale for each n. - (Locally integrable) A non-negative and increasing process X is locally integrable if there exists a sequence of stopping times
 n increasing to infinity, such that
n increasing to infinity, such that 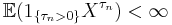 for each n.
for each n.
Types of stopping times
Stopping times, with time index set I = [0,∞), are often divided into one of several types depending on whether it is possible to predict when they are about to occur.
A stopping time  is predictable if it is equal to the limit of an increasing sequence of stopping times
is predictable if it is equal to the limit of an increasing sequence of stopping times  n satisfying
n satisfying  n <
n <  whenever
whenever  > 0. The sequence
> 0. The sequence  n is said to announce
n is said to announce  , and predictable stopping times are sometimes known as announceable. Examples of predictable stopping times are hitting times of continuous and adapted processes. If
, and predictable stopping times are sometimes known as announceable. Examples of predictable stopping times are hitting times of continuous and adapted processes. If  is the first time at which a continuous and real valued process X is equal to some value a, then it is announced by the sequence
is the first time at which a continuous and real valued process X is equal to some value a, then it is announced by the sequence  n, where
n, where  n is the first time at which X is within a distance of 1/n of a.
n is the first time at which X is within a distance of 1/n of a.
Accessible stopping times are those that can be covered by a sequence of predictable times. That is, stopping time  is accessible if, P(
is accessible if, P( =
= n for some n) = 1, where
n for some n) = 1, where  n are predictable times.
n are predictable times.
A stopping time  is totally inaccessible if it can never be announced by an increasing sequence of stopping times. Equivalently, P(
is totally inaccessible if it can never be announced by an increasing sequence of stopping times. Equivalently, P( = σ < ∞) = 0 for every predictable time σ. Examples of totally inaccessible stopping times include the jump times of Poisson processes.
= σ < ∞) = 0 for every predictable time σ. Examples of totally inaccessible stopping times include the jump times of Poisson processes.
Every stopping time  can be uniquely decomposed into an accessible and totally inaccessible time. That is, there exists a unique accessible stopping time σ and totally inaccessible time υ such that
can be uniquely decomposed into an accessible and totally inaccessible time. That is, there exists a unique accessible stopping time σ and totally inaccessible time υ such that  = σ whenever σ < ∞,
= σ whenever σ < ∞,  = υ whenever υ < ∞, and
= υ whenever υ < ∞, and  = ∞ whenever σ = υ = ∞. Note that in the statement of this decomposition result, stopping times do not have to be almost surely finite, and can equal ∞.
= ∞ whenever σ = υ = ∞. Note that in the statement of this decomposition result, stopping times do not have to be almost surely finite, and can equal ∞.
See also
- Optimal stopping
- Odds algorithm
- Secretary problem
- Hitting time
- Stopped process
- Disorder problem
- Parking problem
- Quick detection
- Début theorem
References
- Chung, Kai Lai (1982). Lectures from Markov processes to Brownian motion. Grundlehren der Mathematischen Wissenschaften No. 249. New York: Springer-Verlag. ISBN 0-387-90618-5.
- Fischer, Tom (2011). "Stopping times are hitting times: a natural representation". arXiv:1112.1603 [math.PR].
- Revuz, Daniel and Yor, Marc (1999). Continuous martingales and Brownian motion. Grundlehren der Mathematischen Wissenschaften No. 293 (Third edition ed.). Berlin: Springer-Verlag. ISBN 3-540-64325-7.
- H. Vincent Poor and Olympia Hadjiliadis (2008). Quickest Detection (First edition ed.). Cambridge: Cambridge University Press. ISBN 9780521621045.
- Protter, Philip E. (2005). Stochastic integration and differential equations. Stochastic Modelling and Applied Probability No. 21 (Second edition (version 2.1, corrected third printing) ed.). Berlin: Springer-Verlag. ISBN 3-540-00313-4.
Further reading
- Thomas S. Ferguson. “Who solved the secretary problem?”, Stat. Sci. vol. 4, 282–296, (1989).
- An introduction to stopping times.
- F. Thomas Bruss, “Sum the odds to one and stop”, Annals of Probability, Vol. 4, 1384–1391,(2000)